☰ Home

Tujuan

  • Siswa mampu menentukan nilai Titik Potong, Sumbu Simetri dan Titik Puncak

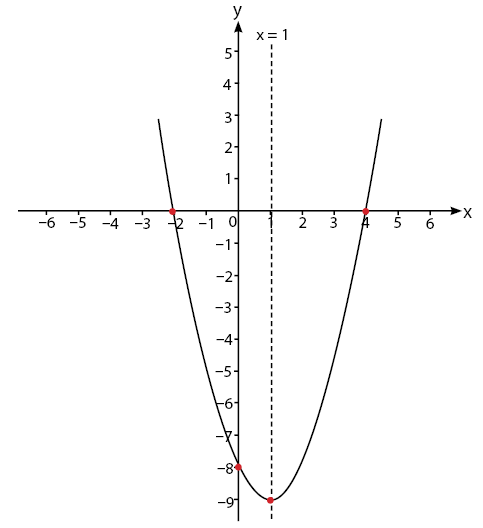
Titik Potong Grafik

Sumbu-$x$
Sebuah grafik fungsi akan memotong sumbu-$x$ jika nilai $y=0$. Jadi, titik potong sumbu-$x$ akan diperoleh jika $ax^2+bx+c=0$.
Sumbu-$y$
Jika sebelumnya grafik fungsi kuadrat akan memotong sumbu-$x$ ketika $y=0$, maka sebaliknya sebuah grafik fungsi akan memotong sumbu-$y$ jika nilai $x=0$.

Sebelumnya 1 2 3 Selanjutnya

Sumbu Simetri & Nilai Optimum

Sumbu Simetri

Garis yang membagi dua bagian grafik fungsi kuadrat secara simetris seperti tampak pada gambar diatas disebut sumbu simetri fungsi kuadrat yang dapat dicari dengan :

Sumbu Simetri$=-\frac{b}{2a}$.

Nilai Optimum
Nilai optimum adalah nilai maksimum atau minimum dari suatu fungsi $f(x)$. Rumus nilai optimum adalah.
$f(x)_p=-\frac{b^2-4ac}{-4a}$

Sebelumnya 1 2 3 Selanjutnya

Titik Puncak / Titik Balik

Koordinat titik puncak sering juga disebut koordinat titik balik. Koordinat ini ada 2 macam yaitu :
  • Koordinat titik balik maksimum terjadi jika $a<0$.
  • Koordinat titik balik minimum terjadi jika $a>0$.
Titik puncak / titik balik grafik fungsi kuadrat berada pada koordinat :
(Sumbu Simetri, Nilai Optimum)

Sebelumnya 1 2 3 Selanjutnya

Mari Mencoba

Untuk lebih memahami bagaimana cara mencari titik potong, sumbu simetri, niai optimum, dan titik puncak. Coba kalian simak animasi dibawah ini.



*Tunggu sampai tombol mulai muncul